Url shortener
Introduction
In this example, the major concepts we’ll be going through are:
- Encoding / address space
- Unique id generation. This will be a precursor to sharding, what a good/bad sharding scheme is, and eventually give us better understanding consistent hashing.
- Caching (but not chained object cache-invalidation)
- Digressions into performance tuning, IOPS, random numbers, counters, encoding, and compression.
How to use this
You’ll need a pencil and paper to do calculations and draw diagrams. A diagram contains 4 things …
Table of Contents
Scenario
We want to make an url shortener aka. a service that takes long urls http://thebestpageintheuniverse.net/ and turns them into something shorter. Assume we need to store a billion urls / month for 10 years with a 25 ms response time. The short url should be no longer than 10 characters long.
Design a system for an SLA of 99.95 and answer some basic questions:
- What is the system?
- How much will it cost (dev, qa, operations)?
- Given that the system will need to become more robust over time - how would the system be built to start vs the final state?
- Up to what point will it scale?
- How fast will it recover from a fault?
The Process
- Design phase - understand the problem and make some estimates for the items we do not know yet. Come up with several designs that may work.
- Compare the designs - part 1 . Find any arbitrary limits on the application design, the fault tolerance, and recovery. Find any limits on the cpu, memory, network (bandwidth, tcp connect, etc), disk (iops, storage, fd, etc).
- Compare the designs - part 3 . Look at 100x and analyze the performance, cost, and scalability at avg and peak loads. Think big. Scale down. Remember we want to minimize the total amount of work we have to do or at least know when we should be doing the work. At this point, also understand the cost of maintenance and code changes.
- Profit.
Design phase
Hint 1
Figure out how to generate the short url of less than length 10 and convert it back to a URL before doing any extensive analysis.
Hint 2
This breaks down into several operations.
- The generation of a unique id
- The mapping of the id into a short_url that is less than 10 characters long
- The storage and retrieval of the id + long_url
Come up with several different designs. If you don’t have pencil and paper, you should probably get some and start drawing diagrams. Reading through this without doing anything is probably a waste of time.
There are a few ideas that can be found be moving the operations around to different components of the system.
- The generation of a unique id
- The mapping of the id into a short_url that is less than 10 characters long
- The storage and retrieval of the id + long_url
Generation of the unique id:
- Generate an id on the application side and attempt to insert it. If there are multiple applications, we’d have to implement this everywhere.
- Generate an id in a 3rd system and attempt to insert it. If there are multiple systems needing a unique id, this may be the way.
- Write the url to the database and auto-increment the primaryid.
For systems 1 and 2, we need to still guarantee the uniqueness or we may have to account for retrying on collisions. In the simplest form, this could be using an MD5/SHA of the long-url or generate a UUID.
Mapping of the id to short_url less than 10 characters long:
This needs to be a 1-1 mapping. Whether this is a 64-bit int primary key in the database or a UUID, we can use encoding (base64) to shorten it up to the required length and give this out to the user as our short url.
Make some guesses/estimates - what are the performance and scalability limits of this problem?
Let’s make a few assumptions regarding the scale up and do some rounding for convenience.
- The maximum size of a URL is 512 bytes and the short url can only be 10 bytes. We can estimate this as 500 bytes / url.
- The number of reads is 10 times the number of writes.
- At some point in time, we have 100x more load on the system.
- The number of seconds in a day is 86400 which we’ll estimate as 1e5.
Make a table and compare in the next step.
Initial estimate
| Year | 1 | 10 |
|---|---|---|
| Total urls / year | \(1E9*12 month =12E9\) | 12E9 |
| Cumulative urls | 12E9 | 120E9 ~= 1E11 |
| Total uncompressed storage | \(500 bytes *12E9 = 6E12\) | 500E11 ~= 50E12 (50 TB) |
| Total compressed storage | 3E12 = 3TB | ~= 25E12 (25 TB) |
| Writes / second | \(1E9/1E5/30 = 333\) | 333 |
| Reads / second (100x writes) | 3333 | 3333 |
| IOPS / second | ~ 4000 | 4000 |
100x
| Year | 1 | 10 |
|---|---|---|
| Total urls / year | \(1E11*12 month =12E11\) | 1.2E12 |
| Cumulative urls | 12E11 | 12E12 ~= 1E13 |
| Total uncompressed storage | \(500 bytes *12E11 = 600E12 = 600 TB\) | 500E13 ~= 5E15 (5 PB) |
| Total compressed storage | 300E12 = 300TB | ~= 2.5E15 (2.5 PB) |
| Writes / second | $1E11/1E5/30 = 1E5/3 = 3.33E4 | 33E3 |
| Reads / second (100x writes) | 333E6 | 350E3 |
| IOPS / second | ~ 400000 = 400E3 | 400E3 |
Note that depending on our storage medium, a write could take anywhere between 1 IOP and 3 IOP. We’re roughly ballparking requirements, so we don’t need a high-level of precision. See IOPS for more details.
Another thing to note is that the worst-case storage requirements are 5 PB. We’ll need to calculate the cost tradeoff between disk vs cpu for compression. We’re growing at approximately 3PB / year if we compress the data.
Comparison / Analysis phase - first pass
We have a few ideas of designs and we have the requirements for the initial launch and 100x the traffic. We need to first examine the system for the initial requirements.
Overall application design limits - what is the total address space we need for the system?
We need to store a total of 1E13 urls. First, we need to know the total number of bits we need to represent this.
Since \(2^{10} = 10^{3}\), we need a total of
1013 = 210 * 210 * 210 * 210 * 10
~= 244
This means we need approximately 44 bits of address space to store all of our URLs over the lifetime of the system.
Design 1 Analysis
Let’s start with the shared-nothing id generation (generate in client) since it would appear to be the most scalable.
Design 1 - 4x1 diagram
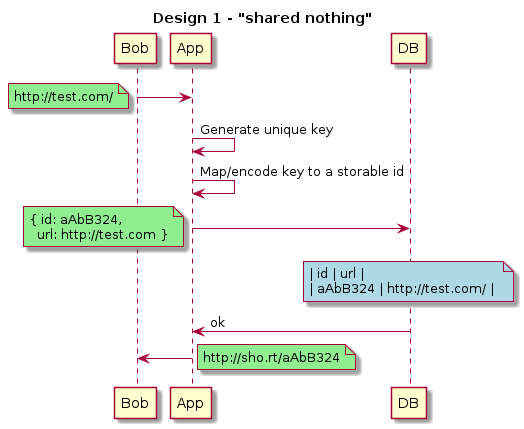
Application design limits - how are we guaranteeing that the short url is less than a length of 10?
We need to generate a unique key and the easiest way of doing so could be taking an md5/sha/uuid of the long url. Then we map/encode the key and store it.
An MD5/SHA/UUID is \(32 hexchar * 4 bits/hexchar = 128 bits\)
For the best user experience, we would like to just have the characters [a-z0-9] - which would give us base36 encoding. If we use [a-zA-Z0-9], that would be base 62 encoding, however, we’ll be using base64 to do our estimations as \(64 = 2^6\)
We need to figure out the total length of the short url based on an 128 bit id.
base2 representation, the total length would be 128. We can imagine this as a set of 128 elements each having values 0 or 1.
base16 representation, a hex value is 4-bits. Each character now represents \(2^4 = 16\) values. We can group the 128 elements into groups of 4. This would be 32 groupings. In mathematical terms, 2128 = (24)32 . 32 hex characters is the standard representation of a UUID/md5/sha.
base64 representation \(2^{128} = (2^6)^x\) . Taking \(log_2\) of each side, \(x = 128⁄6 ~= 21\)
Even in base64 representation, a 128-bit id will be represented by 21 - base64 characters.
We need to make sure that we can store \(10^{13}\) in the worst case scenario of 100x more traffic.
We should calculate the maximum address space available to us for 10 elements:
- base32 -> \((2^5 )^{10} = 2^{50} = (2^{10})^5 = (10^3)^5 = 10^{15}\)
- base64 -> \((2^6) ^{10} = 2^{60} = (2^{10})^6 = (10^3)^6 = 10^{18}\)
- 1013 in base32 -> \(10^{13} = (2^5)^x\) . Then taking \(log_2\) again, \(13 * log_2(10) = 13 * 3.5 = 5 * x\) and \(x \approx 9\)
- 1013 in base64 -> \(10^{13} = (2^6)^x\) . Then taking \(log_2\) again, \(13 * log_2(10) = 13 * 3.5 = 6 * x\) and \(x \approx 8\)
Given that we need about 8 characters of [a-zA-Z0-9] and 9 characters of [a-z0-9], using base32 probably provides a better user experience.
Since we calculated we only need 44-bits earlier, we can use a 64-bit key. There are other hashing functions such as murmur or fnv which are fast and support lower bit-lengths.
Let’s quickly look through the other designs.
Design 2 Analysis
The second design requires a 3rd system involved. We want to explore a different pattern than design 1, so naively, this could be a system which gets generates sequential ids and sends them back to our app servers.
Design 2 - 4x1 diagram
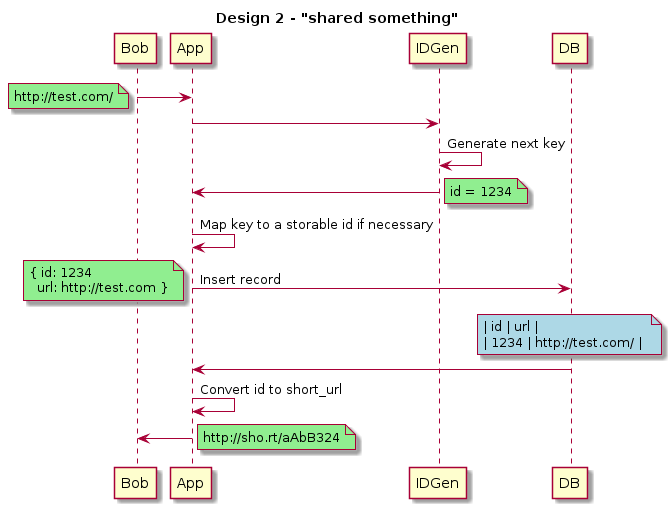
Application design limits - can we autoincrement fast enough?
In this case, we are essentially going to make a single counter. Incrementing a counter in memory takes about 0.2-0.3 microseconds given it should take 2 memory accesses and an addition. This is \(0.3 * 10^{-6} = 3 * 10^{-7}\) . This would give \(0.33 * 10^7 = 3.33 * 10^6\) increments in a second. A rough guesstimate of 3 million in a second or 3333 increments per ms. Note that this is for single threaded counter. With a multi-threaded counter, we’d have to deal with locks on the memory if we wanted accuracy or the counter to be atomic, which we need to have to guarantee uniqueness.
Although our memory is fast enough, the bottleneck occurs somewhere else. From redis benchmarks, the incr operations maxes out at 150e3 requests per second. In our first phase of the lifecycle, we only need to do 333 writes per second on average and 3333 writes per second on peak (10x).
At this point, this design requires a 3rd component, so let’s avoid the extra complexity unless necessary. We’d need to figure out how to make this resilient, which could be tricky.
Design 3 Analysis
The third design involves using a relational database to autoincrement an id and then we can encode it into a short url. Generally, using an RDBMs for the first phase of the application lifecycle works pretty well.
Design 3 - 4x1 diagram
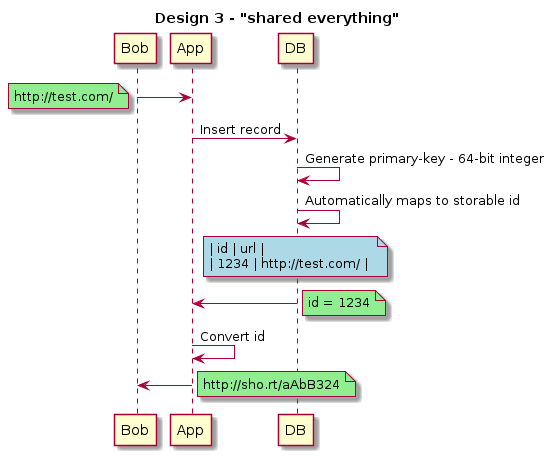
Application design to physical limits - is there a problem?
We already examined the application limits, we know the address space works fine as we need 44-bits and we can have 64-bit indexes.
From the initial requirements table we need to have a total of 50TB of storage and support a total IOPS of 4000 or 40000 at peak.
An EBS volume (gp2) can be up to 16TB with 10k IOPS per volume. And naively, we can put 23 such volumes onto a single machine. The total storage over 10 years is approximately 60 TB. Hopefully, having 5 such volumes would work. Naively, the from a IOPS and disk storage can be managed on a single machine. From Aurora benchmarks, a machine can do 100k writes and 500k reads with a r3.8xlarge with 32 cores and 244 GB memory, so the cpu should also be fine at the database layer. Finally, the network would be at peak \(40000 * 500 bytes = 4 x 10^4 * 500 = 2000 * 10^4 = 20 * 10^6 = 20 MB/s\) . Most systems have gbit links, so even with multiple slaves, this should not be an issue.
The app should only take a few ms and then we are hopefully in an epoll loop at the database end. The entire request cycle should be around 10 ms, the main question is how much context-switching would affect the overall throughput. Naively, we can say each core can handle \(1 / (10 ms / request) = 100 requests/sec\) . This would mean at average we need 40 cores and at peak 400 cores. However, we know it should be much less because of the epoll loop. The application side encode/decode/http-request handling/db query should be on the order of ms. Benchmark your own code to confirm.
This covers the cpu, memory, network, and disk on the app and database. Regarding fault tolerance, we need to have a standard master-slave situation. Automated failover ranges from 30s to 90s.
For the initial requirements, this is the simplest design from a development and maintenance perspective also.
Comparison / Analysis phase - second pass - scaling and performance
Of the three main operations we are doing, in the first pass, we didn’t look in depth at the storage because in design 3 we showed that naively the data can fit on a single database server. If we have to support 100x on the storage layer, we need to store 5 PB of data. We need to understand how to shard the data, what is shared, and how to make sure there are no hotspots.
Design 3
In this design, we were storing the data and generating the id in the data layer. Since we know we need to shard to multiple databases, what is the sharding scheme such that the id’s are unique?
How to scale this up?
What is the size of the pre-shard such that we don’t run out of connections?
One idea is that we can use different sequence numbers on each database:
- Even and odd id generation on different databases
- Have each id generated start with a prefix based on the database.
This is essentially a pre-sharding scheme as the number of databases will need to be known beforehand.
Given that we need 5 PB of data, assuming that we have a maximum of 50TB of data per machine, this means we need 100 machines. This accounts for the storage volume and the overall iops, given that we don’t have any hotspots. The memory and cpu also should be approximately the same as our previous analysis.
We have to handle 400k IOPS on average and 4m IOPs at peak for reads and writes. If we can avoid hotspots, each shard will need to handle \(4 x 10^6 / 1 x 10^2 = 4 x 10^4\) . Naively, we may be able to handle peak load, but this is something that would have to be performance tested. Alternatively, we can add caches to reduce the read load, which we’ll need to handle the hotspots in any case, and keep our shard count to the minimum required for disk space.
We still need to reconsider the number of network connections and the number of app servers that we have. Given 100 shards and assuming 20 tcp connections can handle the number of requests, for each app server we would need $tcp_connection_pool_count x db_shard_count = 20 x 100 = 2000 $ . On the database end, we have app_server_count * tcp_connection_pool_count = total_connections
The next step is to understand how many app servers we need. Previously, we calculated that we need 400 cores at peak, now we would need 40k. Given 40 cores per machine, that would be 1000 app servers needed. On each database, we would have 20000 active connections for the database pool. To solve this problem, we need to add an additional layer of abstraction. This would either be a consolidated database pool between application servers or we would have to pin a set of app servers to a set of database shards or we need to move this to the client side on the request and solve this via dns.
Need a diagram describing 3 states:
- just sharded databases - how does the appserver go to the db for a particular hash?
- dns lb
- app pinning for certain urls
Design 1
This was the shared nothing design where we could use a 64-bit hash.
How to scale this up? Can we do better than a hash?
From the previous design, we know we need 100 shards of 50 TB. We can use the first 10-bits to represent 1024 shards, but only use the correct amount aka 100. Note that if we are using a database that represents its data as a binary tree, this will cause some write amplification on some inserts where the child pages need to be split. With a binary tree index, we are trading off random writes for easier reads. Because the hash is essentially random, the IO patterns will be mostly random, which is much slower than sequential. In fact, there are old bugs with mysql such that UUID insert performance decreases with the number of keys.
Unix-timestamp is 32-bit - which lasts from the year 1970 to 2038. Also, we can start our count from a custom epoch like 2018 instead of 1970.
We would like to include milliseconds which can be represented by 10 bits (\(2^{10} = 1024\))
64-bits total:
- 10-bits for number of shards = 2^10 = 1024 - random - we don’t want a bad hash - still can have hotspots.
- 42-bits for time in milliseconds = 70 years of time from custom epoch. We can possibly reduce the bits here since we don’t need 70 years.
- 12-bits = 2^12 = 4096 values per millisecond. We need to atomically increment a counter in some layer for this to work.
This design will allow 4k writes per ms per shard . Very conveniently, we previously calculated that we can increment a counter on a single machine around 3.5k/s. We can pre-shard to 1024 and distribute over 1 machine to start, then slowly ramp it up to n-machines as necessary.
Also, in addition to perhaps being a faster insert, another interesting property of this is that it is roughly ordered..
Design 2
This was having a 3rd system to generate the id.
How to scale this up?
In this case, in our worst case scenario of 100x traffic x 10x peak, we’d have 333e3 requests per second.
We can still make this design work by:
- batching out groups of 10 elements and doing the rest of the counting on the app servers
- having multiple id servers - 10 servers each serving id’s of mod 10.
Also, as a side note to get faster counters, we can do sloppy counting (equivalent of batching) per CPU and try to use the L1 cache, but most applications don’t need such a hard limit.
Random ways to fail
Bad sharding schemes
- Customer/Tenant - one of them could be hot
- Geography - NY - why take a chance?
- By some supernode - goes for graph databases also
Reach arbitrary limit
- tcp connections
- random number generator - what is the limit?
- number of open fd’s
Analysis and tradeoffs so far
We’ve analyzed three different designs so far and it appears that the dynamically generating a unique id and then inserting it appears to be the best approach for now. We have a tradeoff for the speed of inserts on the dynamically generated id which is roughly sortable vs using a hash.
Issues we haven’t tackled yet:
- sharding randomness
- how to avoid hot spots
- maintenance cost of sending modifying shards / multi-database
- TODO - DynamoDB cost vs Aurora cost
WIP - Other questions
Do we even need a cache? Calculate the depth of the btree to figure out seeks. Branching factor of 500 (500 references to child pages, 4kB pages, depth of 4)
How do you know something is hot? Sloppy local counter that gets merged every x minutes + bloom filter?
Size of index (number of rows vs ondisk size):
\[ 500^4 \approx (2^9)^4 = 2^36 = 64 * 10^9 = 64 GB \]
Total storage is: \[ 500^4 * 4kB \approx (2^9)^4 * 4kB = 2^{36} * 4 * 2^{10} = 2^{48} = 2^{8} * 2^{40} = 256 * 10^{12} = 256 TB \]
Would a trie or a hash be better for the k/v lookup for the cache? What is the space/performance tradeoff?
Would your design also support counting the number of hits to a particular url?
In this case, the number of writes > reads.
Questions - can we support the writes directly? If not, can we do batching? How accurate does the count need to be over what time? What is our maximum data loss? Introduction to CRDT - sum-only - eventually consistent.
How would you handle expiry and the cleanup?
At what incoming rate would the design start rejecting write requests? Read requests?
How would you handle multi-region?
- Affinity
- Split shards across regions and do replication across even/odd shard numbers
- Write queues and read caches (hub + spoke) model - could have issues with consistency
- How do you guarantee consistency at a latency of 25 ms? What happens afterwards?
Url compression - use earlier in example? Custom url - race condition - OCC? Spam protection? What is the upgrade strategy if we want to do 10^10 more urls? Can we reuse the same base encoding scheme? In addition, need statistics on the access of each url. How would the answer change if urls expired?
Appendix
Discussion of bits, bytes, and conversion
1-byte conversion (8-bits)
Let’s say in decimal we have the number 129.
Binary (base2) conversion - max value is 255 (2^8-1) 1000 0001 = 2^7 + 2^0 = 129
Hex (base16) conversion - max value is 255 (16^2 - 1) 1000 0001 = 81 8 1
129 = 8*16^1 + 1*16^0 => 81
What is 129 in base36
Numbers + a-z (base36) conversion
129 = 4*32^1 + 1*32^0 => 41
How many single digit integers fit into a byte?
ASCII values of 0-9 are 30-39 in hexadecimal. The representation of a number in ASCII needs 6-bytes, but uses a full-byte and can only represent the numbers 0-9.
However, a single byte has 8-bits and can represent the values from 0-255.
A 4-bit value can represent any value from 0-15, so we can actually fit two digits into a single byte.
Packed binary-coded decimal => 2 numbers can fit into 8 bits, one in the higher bits, one in the lower. Aside - BCD is generally advantageous to do digit by digit conversion to a string while binary representation saves 25% space. Can also assign different values to each bit - instead of 8/4/2/1 can have 8/4/-2/-1.
8-bit clean => 7-bits for data transmission, last one for flag 7-bits of ASCII? 32 - 64 - standard ( 8-bits only, easy to copy/paste) 85 - adobe 91 - base91.sourceforge.net
IOPS - IO operations
To read and write from a disk, first it needs to “move” to the correct position and then read/write the element to the disk. The movement is known as the “seek time” and the second component is the latency which also depends on the size of the sectors and buffers.
The number of IOPS can be described by \(1 / ( seek + latency)\) . However, since \(latency = f(workload)\) and changes over different patterns it is difficult to have precision in knowing the limits of an IO subsystem. Sequential workloads have much higher throughput than random, in-place updates/writes are different than appends, etc.
An 2009 ACM report shows sequential workloads are 3x faster.
If it is a log-structured merge tree, we are trading off having fast sequential writes for random read behaviour (and later we can optimize the random read behaviour with bloom filters, hardware caches, etc) vs a binary tree which does in place updates (random io on writes instead of read).
As a rough estimate:
| Device | IOPS | Interface | Notes |
|---|---|---|---|
| 5,400 rpm SATA | ~15-50 IOPS[2] | SATA 3 Gbit/s | |
| 7,200 rpm SATA | ~75-100 IOPS[2] | SATA 3 Gbit/s | |
| 10,000 rpm SATA | ~125-150 IOPS[2] | SATA 3 Gbit/s | |
| 10,000 rpm SAS | ~140 IOPS[2] | SAS | |
| 15,000 rpm SAS | ~175-210 IOPS[2] | SAS | |
| SSD | ~10000 IOPS |
See https://en.wikipedia.org/wiki/IOPS for more details.
Powers of 2
| Power | Value | Approximation | Short |
|---|---|---|---|
| 10 | 1024 | 1e3 | 1KB |
| 16 | 65536 | 65e3 | 64KB |
| 20 | 1048576 | 1e6 | 1MB |
| 30 | 1e9 | 1GB | |
| 40 | 1e12 | 1TB |
